SEMANA DEL 4 AL 8 DE OCTUBRE

 MAGNITUD DE UN ANGULO (SEMANA DEL 4 AL 8 DE OCTUBRE)

Los ángulos están representados por una magnitud que puede ser analizada y comparada con otras, por lo que existen operaciones entre ángulos. Se puede sumar y restar ángulos entre sí o multiplicarlos y dividirlos por números enteros.

La recta que divide en dos partes iguales a un ángulo se llama bisectriz y cualquier punto de ella equidista de ambos lados del ángulo.

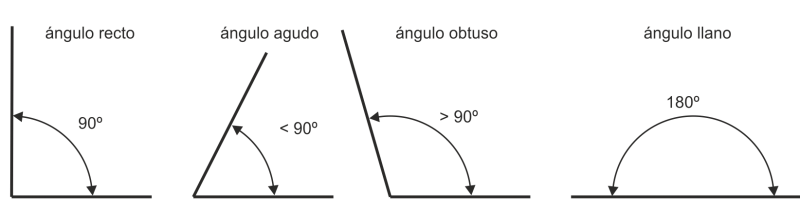
Tipos de ángulos

Un ángulo nulo es el que mide 0°.

Los ángulos se pueden clasificar de acuerdo a ciertos criterios.

Según su amplitud:

• Ángulo nulo. Es el que mide 0°.
• Ángulo agudo. Es el que mide entre 0° y 90°.
• Ángulo recto. Es el que mide 90°.
• Ángulo obtuso. Es el que mide entre 90° y 180°.
• Ángulo llano. Es el que mide 180º.
• Ángulo cóncavo. Es el que mide más de 180°.
• Ángulo completo. Es el que mide 360°.

Según la relación con otro ángulo:

• Ángulos suplementarios. Son ángulos que suman 180º.
• Ángulos complementarios. Son ángulos que suman 90°.

Según su posición:

• Ángulos consecutivos. Son ángulos que comparten un lado y el vértice.
• Ángulos adyacentes. Son ángulos consecutivos y el lado que no comparten forma parte de la misma recta.
• Ángulos opuestos por el vértice. Son ángulos que comparten el vértice pero ninguno de los lados.

Operaciones con ángulos

• Sumas entre ángulos. Cuando se suman dos o más ángulos se deben sumar los grados (y también los minutos y los segundos si corresponde) de cada uno de los ángulos. Por ejemplo:
  ángulo α + ángulo β = ángulo γ
  90º      +      70º     = 160º
• Restas entre ángulos. Cuando se restan dos o más ángulos se deben restar los grados (y también los minutos y los segundos si corresponde) de cada uno de los ángulos. Por ejemplo:
  ángulo γ – ángulo β = ángulo α
  160º     –     70º    = 90º
• Multiplicaciones con ángulos. Cuando se multiplica un ángulo por un número natural se deben multiplicar los grados, los minutos y los segundos por ese número. En el caso de que los valores de los minutos o segundos supere los 60, se deberán pasar esas unidades a la siguiente escala. Por ejemplo:
  ángulo α = 40º 10’ 20”
  ángulo α x 2 = 40º x 2 + 10’ x 2 + 20” x 2 = 80º 20’ 40”
• Divisiones con ángulos. Cuando se divide un ángulo por un número natural se deben dividir los grados, los minutos y los segundos por ese número. Al comenzar, se dividen los grados por el número y el resto que se obtiene se transforma en minutos (al multiplicarlo por 60) y se agrega a los minutos que ya se tenían. Se dividen los minutos y el resto se agrega a los segundos que ya se tenían que luego se dividen.

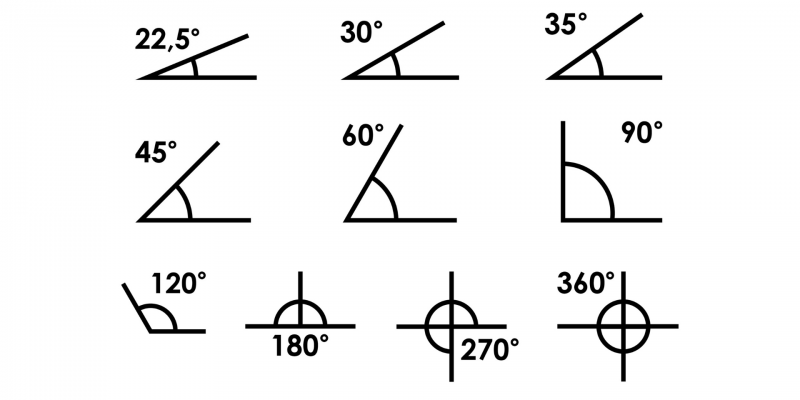
¿Cómo se mide un ángulo?

Para medir la amplitud de un ángulo, se necesita un instrumento de medición llamado transportador. El transportador está graduado, puede ser circular o semicircular y suele ser de plástico. Los pasos para medir un ángulo son:

1. 1. Se debe colocar el centro del transportador, que suele estar indicado con una ranura, en el vértice del ángulo (el origen del ángulo).
2. 2. Luego se debe corroborar que uno de los lados del ángulo coincida con la base del transportador.
3. 3. Se marca la graduación del lado restante en el transportador y esa es la amplitud del ángulo.

- Fuente: https://concepto.de/angulo/

NOTA: REALIZA LOS EJERCICIOS DEL COMPLEMENTO MATEMATICO DE LA PAGINA 28, LA PARTE 2 VAS A CONSTRUIR LA SUMA O RESTA EN TU CUADERNO DE NOTAS.